Un esempio di Hidden Markov Model filtering

Recentemente abbiamo realizzato un modello per il riconoscimento dei gestures, sfruttando le posizioni dei landmarks determinate da MediaPipe. L’obiettivo era quello di creare una applicazione per poter utilizzare una lavagna virtuale, sulla quale si potesse scrivere o cancellare a seconda del gesto e della posizione della mano.

Dopo aver allenato un modello per il riconoscimento delle gesture, ci siamo resi conto della possibilità di poter migliorare i risultati delle predizioni, senza bisogno di cambiare il modello.

Consideriamo l’esempio seguente, in cui una mano passa dal gesto del numero uno (”one”) verso un altro gesto (”other”). Ad ogni frame, il modello predice la probabilità che la mano stia eseguendo il gesto “one” oppure “other”:

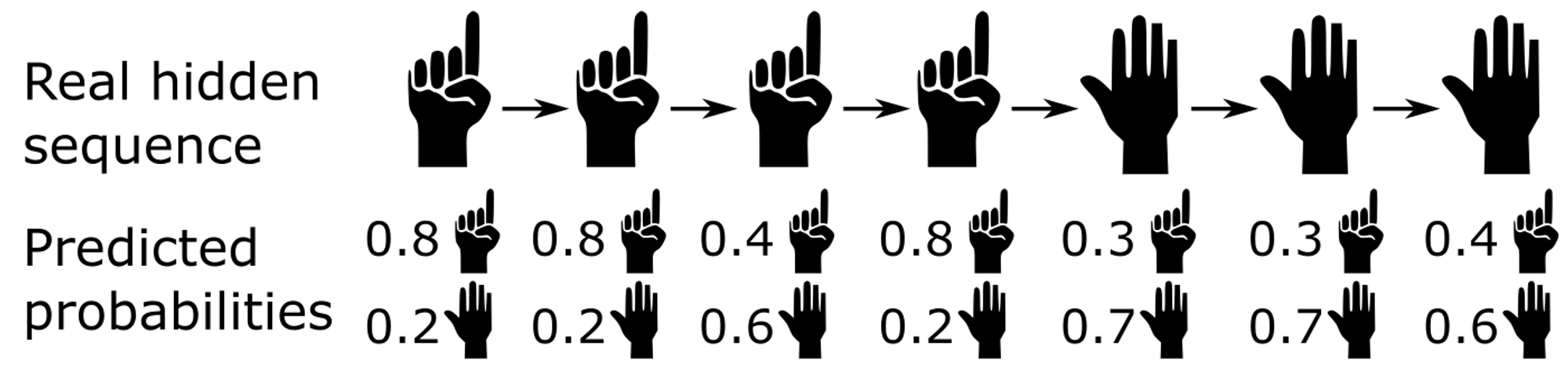
Se ci limitiamo a scegliere ad ogni frame la probabilità più alta, otterremmo le predizioni seguenti (in rosso gli errori).

Si può notare che l’errore nella terza predizione potrebbe essere facilmente evitata. Infatti negli step 1, 2, 4 la gesture “one” viene predetta con probabilità abbastanza alta. Al contrario la predizione al terzo step fornisce “other” con una probabilità abbastanza bassa (60%).

In genere è improbabile che la mano cambi gesture tra due frame successivi, e si intuisci che quindi la predizione dello step 3 sia in realtà un errore del modello. La gesture in realtà non è affatto cambiata.

Queste sono considerazioni intuitive, ma come procedere per formalizzarle ed implementarle in modo efficace (magari il più efficace possibile) in un algoritmo ?

Se avete letto il titolo di questo post conoscete già la risposta: usando un Hidden Markov Model.

Alcune risorse sul teorema di Bayes:

• Spiegazione lunga: https://bayesmanual.com/index.html
• Video da 15 minuti (3B1B): https://www.youtube.com/watch?v=HZGCoVF3YvM
• Altre risorse: https://letmegooglethat.com/?q=bayes+theorem

Le gestures viste come Hidden Markov Model

Riprendendo la definizione di Wikipedia:

Un modello di Markov nascosto (Hidden Markov Model - HMM) è una catena di Markov in cui gli stati non sono osservabili direttamente. Più precisamente:

• la catena ha un certo numero di stati;
• gli stati evolvono secondo una catena di Markov (la probabilità di trovarsi ad un certo stato è determinata dallo stato precedente);
• ogni stato genera un evento con una certa distribuzione di probabilità che dipende solo dallo stato;
• l’evento è osservabile ma lo stato no.

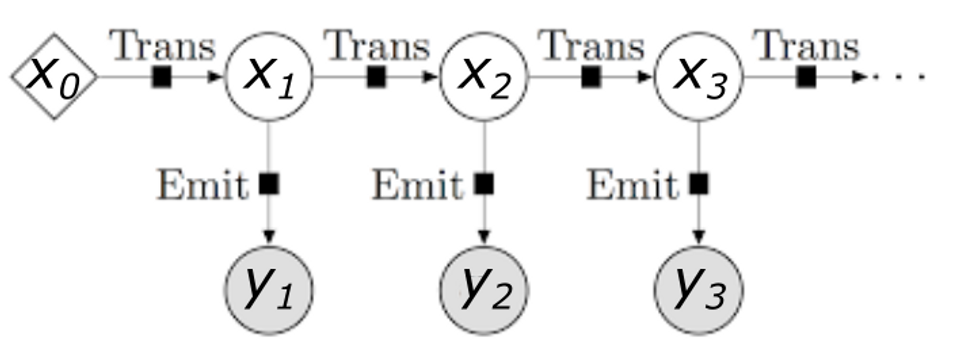
Nel nostro caso gli stati nascosti $x_t$ sono le varie gesture. Per semplificare consideriamo unicamente due gestures: “One” (dito medio alzato e pugno chiuso) e “Other” (qualsiasi altro gesto che non sia one). Nel nostro esempio potremmo utilizzare il gesto “One” per scrivere, usando la punta dell’indice come se fosse una matita virtuale e qualsiasi altro gesto interromperebbe la scrittura sulal lavagna.

Gli stati transiteranno ad ogni frame secondo unadata sequenza, per esempio:

One → One → … → One → Other → … → Other → One → One → …

Supponiamo di conoscere le probabilità secondo la quale il cambiamento di stato si effettua. Lasciamo perdere in che modo: possiamo immaginare di farlo usando una statistica su un dataset, oppure scegliere noi stessi le probabilità manualmente finché il risultato non ci soddisfa.

Per esempio:

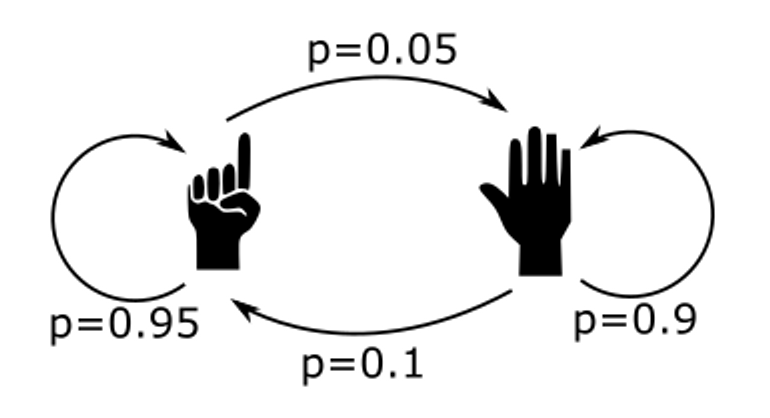
La matrice di transizione sarà:

dove \(A= \left(a_{ij}\right)\) con \(a_{ij}\) la probabilità di transizione da uno stato \(i\) a uno stato \(j\).

Si potrebbe obiettare che le gesture non sono affatto nascoste, dato che la mano è ben visibile davanti ai vostri occhi. Dal punto di vista dell’applicazione però la cosa è lontana dall’essere ovvia, dato che in realtà non può conoscere con certezza quale sia il gesto eseguito dalla mano.

Tutto ciò che osserva infatti sono le posizioni dei landmarks ottenuti dall’escuzione di MediaPipe sul frame. Queste posizioni rappresentano quinid gli osservabili $y_t$, che dipendono, con una certa distribuzione di probabilità, dagli stati (ossia le gesture) $x_t$

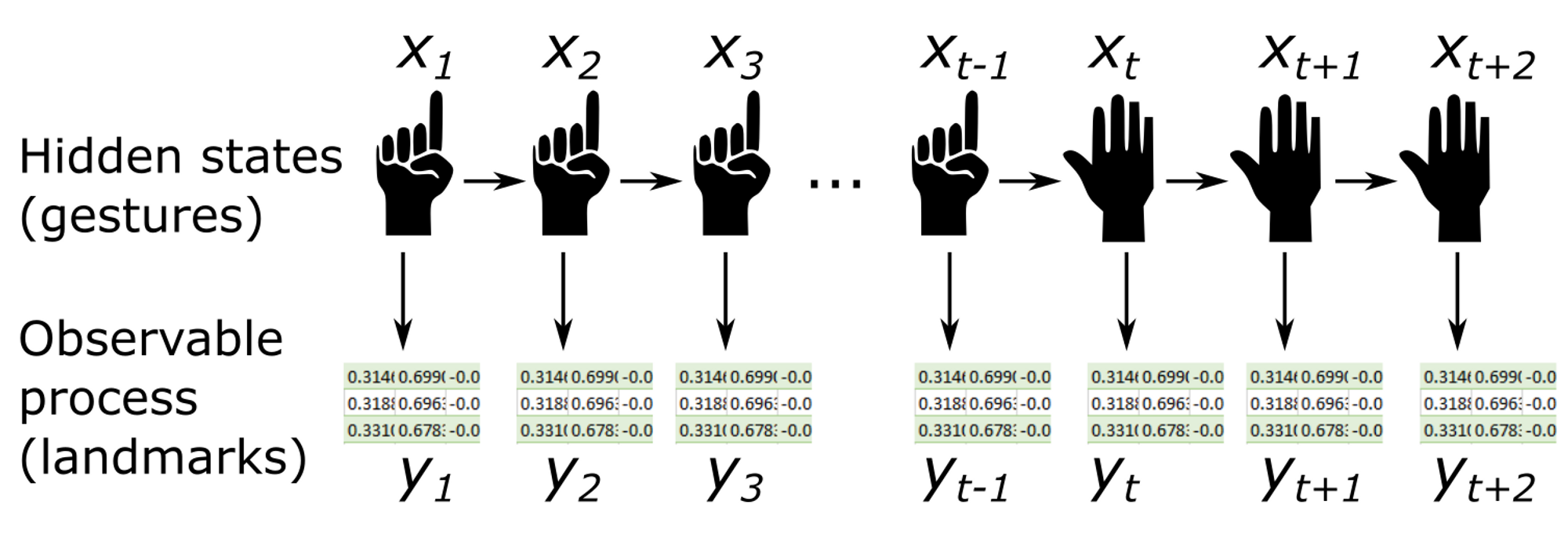
Nonostante possa sembrare che tutti gli ingredienti siano pronti sulla tavola (stati nascosti, matrice di transizione e osservabili) se vogliamo sfruttare l’informazione data dagli osservabili, abbiamo bisogno di conoscere quale probabilità li leghi agli stati nascosti. Abbiamo cioè bisogno di conoscere $P(y_t\mid x_t)$.

La risposta ci viene dall’ultimo ingredient e che non abbiamo ancora aggiunto: il modello di predizione. Abbiamo già detto di avere allenato un modello cha ad ogni frame associ la probabilità che il gesto appartenga alla classe “one” o “other” (attenzione, sto parlando di probabilità, non di logits. Le probabilità si ottengono con un fit specifico o normalizzando le logits a seconda dei casi, esempio: https://datascience.stackexchange.com/a/31045).

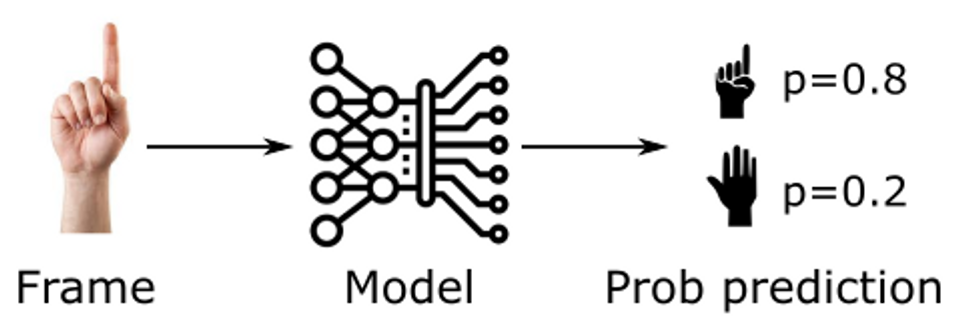
Il risultato dato dal modello è la probabilità di avere un certo gesto, a partire dai landmark osservati, ossia:

Che è esattamente il contrario di ciò che ci serve! Come fare per scambiare i due termini? Usando il teorema di Bayes:

• \(P(x_t\mid y_t)\) facile, è l’output del modello;
• \(P(y_t)\) non lo conosciamo, ed è praticamente impossibile da trovare. Per fortuna non è un problema, infatti troveremo il modo di semplificare questo termine ed eliminarlo dalle nostre equazioni. In realtà ciò che davvero ci serve è poter confronare la probabilità dell’osservabile per i diversi possibili stati nascosti. La probabilità “a priori” dell’osservabile $P(y_t)$ è sempre la stessa e non darà quindi nessun contributo nel favorire un’ipotesi rispetto ad un’altra;

• \(P(x_t)\) per trovarlo bisogna ragionare un po’. Il principio di base dell’utilizzo del HMM, e più in generale di tutti i metodi Bayesiani, è quello di sostituire gli “a priori” del proprio modello, con degli “a priori” più efficienti. In questo caso l’a priori che abbiamo deciso di usare è la catena di Markov e più precisamente la matrice di transizione: ciò che vogliamo fare infatti è realizzare delle predizioni che tengano in conto di queste informazioni.

  Quindi il nuovo “a priori’ è la catena di Markov, ma qual era quello vecchio? Quale “a priori” sullo stato viene utilizzato dal modello, se usato senza nessun tipo di filtro? Se pensate che la risposta sia “nessuno” vi state sbagliando: è infatti impossibile non avere un “a priori”.

  La risposta non è poi così complessa, al di là delle features utilizzate dal modello, vi è un altro dato importanto che viene sfruttato per le predizioni: la frequenza dello stato nel dataset. Infatti, indipendentemente dagli osservabili, il modello tende a predirre con più probabilità stati che sono presenti in maggioranza nel dataset di train. È questo l’”a priori” usato dal modello, l’informazione in funzione della quale vengono fatto le predizioni. Il valore di $P(x_t)$ è la frequenza dello stato $x_t$ nel dataset di train.

  Nel nostro caso abbiamo allenato il modello su quattro dataset, di lunghezza equivalente, rappresentanti quattro gestures diverse (”one”, “closed hand”, “open hand”, “spiderman”). Quindi:

  \(p(x_t=\mbox{"one"})=0.25\) e \(p(x_t=\mbox{"other"})=0.75\)

Ora siamo pronti per implementare il nostro filtro.

Il Forward algorithm

Per questa parte mi rifarò principalemente alla presentazione che viene fatta su Wikipedia (https://en.wikipedia.org/wiki/Forward_algorithm) che ho trovato chiara e ben fatta.

Se il nostro modello di base si limita a calcolare $p(x_i\mid y_i)$, ciò che vogliamo fare è includere l’informazione data da tutti gli stati precedenti, ossia calcolare

NOTE Per semplicità di notazione indicheremo con la scrittura $p(y_1,\dots,y_t):=p(y_1 \cap \dots \cap y_t)$ l’intersezione di tutti gli eventi.

Nonostante l’obiettivo finale sia determinare $p(x_{t}\mid y_{1},\dots,y_{t})$, useremo l’algoritmo per calcolare $\alpha_{t}(x_{t}):=p\left(x_{t},y_{1},\dots,y_{t}\right)/p\left(y_{t}\right)$, in modo da semplificare i calcoli nel processo di induzione. Per riottenere la probabilità cercata applicheremo:

dove $\alpha_{t}:=p\left(y_{1},\dots,y_{t}\right)/p\left(y_{t}\right)$.

Per dimostrate la ricorsione, poniamo:

Dove abbiamo sfruttato il fatto che i vari stati $x_{t-1}$ (ossia le possibili gesture corrispondenti al fotogramma $t-1$) sono mutalmente esclusivi, ed almeno uno di essi deve realizzarsi.

Il teorema della probabilità composta afferma che:

Nel caso di tre eventi $A$, $B$, $C$ diventa:

Applicandolo al nostro caso otteniamo:

Consideriamo i vari termini del prodotto separatamente:

\(p\left(y_{t}\mid x_{t},x_{t-1},y_{1},\dots,y_{t-1}\right)\) è la probabilità dell’osservabile \(y_{t}\) (posizioni dei landmarks) in funzione dello stato nascosto \(x_{t}\) (gesture) e degli osservabili precedenti. Ma in realtà la probabilità di \(y_{t}\) è completamente determinata dallo stato nascosto, ossia la posizione dei landmarks dipende unicamente dal gesto effettuato dalla mano, e non dalle posizioni nei fotogrammi precedenti. Quindi \(p\left(y_{t}\mid x_{t},x_{t-1},y_{1},\dots,y_{t-1}\right)=p\left(y_{t}\mid x_{t}\right)\). In conseguenza di quanto detto precedentemente:

\(p\left(x_{t}\mid x_{t-1},y_{1},\dots,y_{t-1}\right)\) è la probabilità che lo stato attuale sia $x_{t}$ sapendo che lo stato precedente è \(x_{t-1}\) e conoscendo gli osservabili precedenti. Di nuovo, gli osservabili precedenti non ci danno nessuna informazione aggiuntiva rispetto a \(x_{t-1}\). Quindi \(p\left(x_{t}\mid x_{t-1},y_{1},\dots,y_{t-1}\right)=p\left(x_{t}\mid x_{t-1}\right)\) che è dato dal termine corrispondente nella matrice di transizione.

$p\left(x_{t-1},y_{1},\dots,y_{t-1}\right)=\alpha_{t-1}\left(x_{t-1}\right)$ riprendendo le definizioni, il che ci permette di stabilire il passo induttivo nella ricorsione. Quindi otteniamo:

Dove \(p\left(x_{t}\mid y_{t}\right)\) è l’output del modello, $p\left(x_{t}\right)$ è la frequenza dello stato $x_{t}$ nel dtaset di train, $p\left(x_{t}\mid x_{t-1}\right)$ è la probabilità di transizione dallo stato $x_{t}$ a $x_{t-1}$ e $\alpha_{t-1}\left(x_{t-1}\right)$ è l’output dell’algoritmo allo step precedente.

L’unica cosa che ci manca è la base dell’induzione, ossia il valore di \(\alpha_{0}(x_{0})\). Per stabilirlo si può sfruttare una qualche proprietà del processo, per esempio se si conosce con quale probabilità le gesture iniziale si presentano. Nel nostro caso il processo inizia con l’avvio della telecamera: dato che la gesture “one” corrisponde alla scrittura sulla lavagna conviene, per evitare scritture indesiderate, partire con la gesture “other”. Dunque \(\alpha_{0}(x_{0}=\mbox{"one"})=0\) e \(\alpha_{0}(x_{0}=\mbox{"other"})=1\).

In ogni caso l’impatto di \(\alpha_{0}(x_{0})\) sul processo di predizione si estingue rapidamente dopo alcuni secondi e non è quindi un parametro molto importante, permomeno nel nostro caso.

Implementazione

• Puoi trovare i dettagli nel repository Github *

Ecco una dimostrazione del risultato ottenuto: 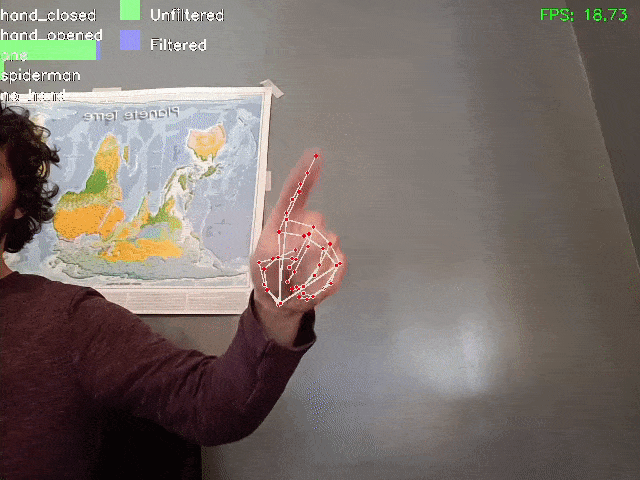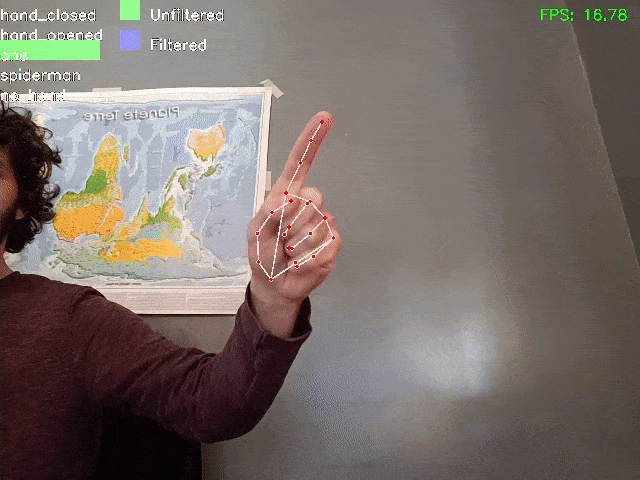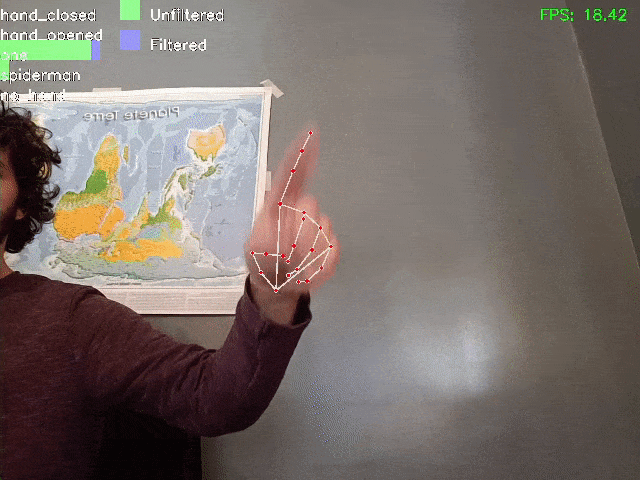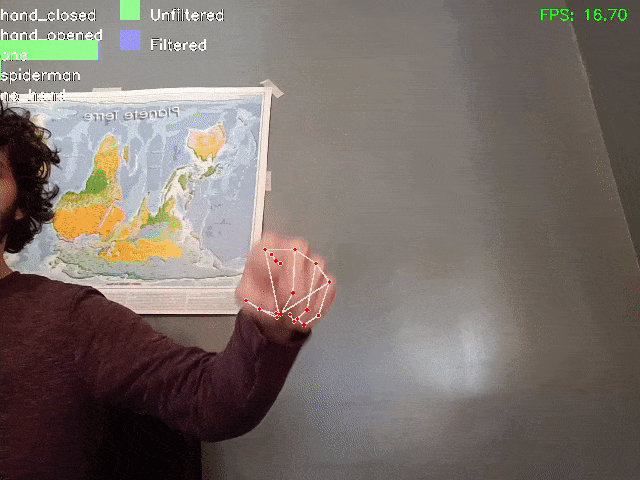Notare che grazie al filtraggio, anche se su alcuni fotogrammi il modello sbaglia (attribuendo il risultato “spiderman” o “mano chiusa”), il risultato filtrato è più stabile e corretto.

Ed ecco la nostra implementazione della classe HMMFiltering:

class HMMFiltering():
    def __init__(self, trans_mat, alfa_0, freqs, model):
        """
        :param trans_mat: Transition matrix of the HMM
        :param alfa_0: Initial values for alpha_t
        :param freqs: Frequencies of the hidden states in model train dataset"""
        self.trans_mat = trans_mat
        self.alfa_0 = alfa_0
        self.freqs = freqs
        self.alfa_t = self.alfa_0

    def update_alfa(self, unfiltered_probs):
        """Calculate alpha_t+1 given the observation y_t"""
        first_coeff = np.array(list(unfiltered_probs.values()) )/ self.freqs
        second_coeff = 0
        for i in range(len(self.alfa_t)):
            second_coeff += self.trans_mat[i] * self.alfa_t[i]
        self.alfa_t = first_coeff * second_coeff
        # Normalize alfa_t to avoid numerical errors
        self.alfa_t = self.alfa_t / sum(self.alfa_t)


    def predict_proba(self, unfiltered_probs):
        """
        Calculate the hidden state probability given the observation y_t.
        Unfliltered_probs is a dictionary in the form {'name_gesture': prob, ...}
        """
        classes = unfiltered_probs.keys()
        self.update_alfa(unfiltered_probs)
        return {gesture: prob for gesture, prob in zip(classes, self.alfa_t/sum(self.alfa_t))}

Lavagna virtuale

Ecco un esempio di HMM filtering applicato alla nostra lavagna virtuale:

Modello semplice:

Con HMM Filtering: